Revision as of 09:54, 6 January 2023

De vlucht van een pijl zonder luchtweerstand

Het traject van een pijl is, bij afwezigheid van luchtweerstand, enkel afhankelijk van de snelheid bij vertrek, de hoek waarin de pijl afgeschoten wordt, de hoogte van waarop de pijl vertrekt, de valversnelling en de hoogte van het eindpunt.
Om de formule te bepalen hebben we dus nodig:
- snelheid $v_{0}$ (in ${\frac {m}{s}})$ )
- valversnelling $g=9.81{\frac {m}{s^{2}}}$ )
- $\theta _{0}$ de hoek waaronder de pijl afgeschoten wordt (in graden)
- begin hoogte (in m)
- eind hoogte (in m)
- $x_{0}$ : horizontale beginpositie
- $x$ = de afgelegde horizontale afstand
- $y_{0}$ : verticale beginpositie
- $y$ = de afgelegde verticale afstand (=hoogte)
De positie van de pijl wordt bepaald door de formule:

$y=y_{0}+tan(\theta _{0})\left(x-x_{0}\right)-{\frac {g}{2v_{0}^{2}cos^{2}\theta _{0}}}(x-x_{0})^{2}$

de maximale afstand, R, die een pijl kan afleggen (zonder luchtweerstand) wordt gegeven door de formule

$R={\frac {v_{0}^{2}}{2g}}\left(1+{\sqrt {1-{\frac {2g}{v_{0}^{2}sin^{2}\theta _{0}}}(x-x_{0})}}\right)sin2\theta _{0}$

Wanneer de begin en eind hoogte dezelfde is, kan formula vereenvoud worden tot:

$R={\frac {v_{0}^{2}}{g}}sin2\theta _{0}$

- Deze afstand is maximaal voor een hoek van 45°. Dan wordt $sin2\theta _{0}$ gelijk aan 1 en is de formule

$R_{max}={\frac {v_{0}^{2}}{g}}$

De tijd ( $T$ ) dat de pijl onderweg is wordt gegeven door de formule

$T={\frac {v_{0}}{g}}\left(1+{\sqrt {1-{\frac {2g}{v_{0}^{2}sin^{2}\theta _{0}}}(y-y0)}}\right)sin\theta _{0}$

De maximale hoogte ( $H$ ) dat een pijl kan bereiken wordt gegeven door de formule:

$H=y_{0}+{\frac {v_{0}^{2}}{2g}}sin^{2}\theta _{0}$

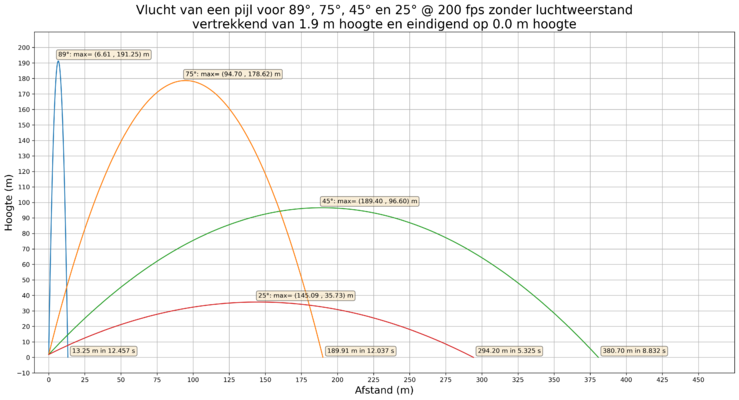
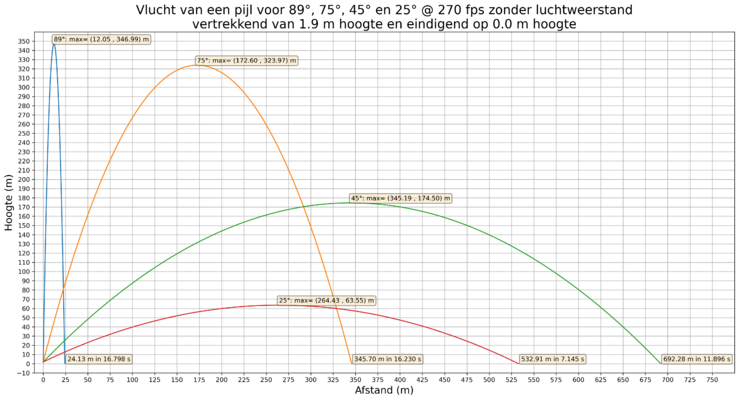
Hieronder staan de trajecten voor een pijl afgeschoten aan 200 fps (links) en 270 fps (rechts).
- De vorm van de trajecten is dezelfde voor de 200 fps en de 270 fps pijl, enkel de hoogte en afstand is verschillend.

Vlucht van een pijl aan 200 fps
Vlucht van een pijl aan 270 fps

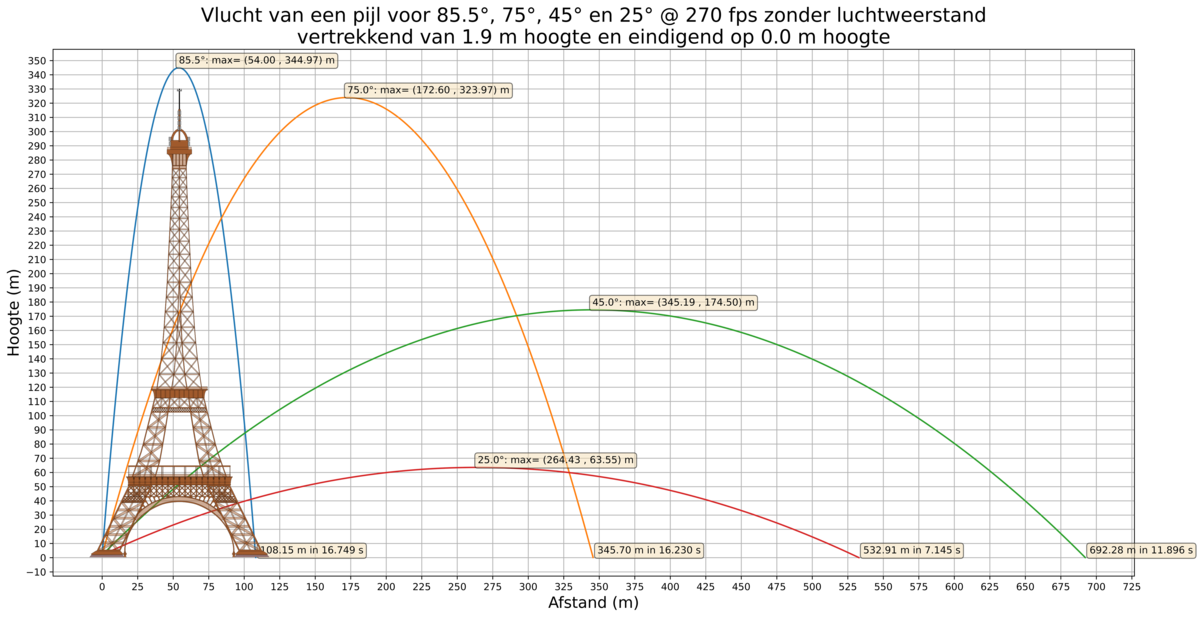
Indien er geen luchtweerstand is, zou je zelfs met een moderne compound boog van 70# gemakkelijk over de Eifeltoren heen kunnen schieten!
- Vandaar altijd zorgen voor een goede pijlenopvang achter het doel, nooit de boog naar boven aanspannen, enz.

Vermits een model zonder luchtweerstand niet realistisch is, dienen we de berekeningen te herhalen met luchtweerstand. (to be continued)

Vlucht van de pijl rekening houdend met de luchtweerstand.

De luchtweerstand voor een object in beweging wordt weergegeven door de volgende formule
- $F_{d}={\frac {1}{2}}\rho v^{2}C_{d}A$
met:
- $\rho$ de dichtheid van het medium waarin het voorwerp zich voortbeweegt, hier de lucht.
- $v$ de snelheid van het voorwerp in m/s
- $C_{d}$ de drag coefficiënt (weerstandscefficiënt)
- $A$ de oppervlakte van de doorsnede loodrecht op de bewegingsrichting
- $F_{d}$ de kracht die uitgeoefend wordt op het voorwerp tijdens de beweging in het medium (lucht)

Hierboven hielden we enkel rekening met de valversnelling in de y-component, moeten we hier rekening houden met de luchtweerstand voor zowel de x- als de y-component van de snelheid.
- $v_{0}$ beginsnelheid
- $\theta$ de hoek waaronder de pijl wordt afgeschoten.
- $vx_{0}=v_{0}cos(\theta )$ de x-component van de beginsnelheid
- $vy_{0}=v_{0}sin(\theta )$ de x-component van de beginsnelheid

We kunnen dus op zowel de x- als de y-component van de snelheid, per klein tijdseenheid dat het voorwerp bewogen heeft, de nodige aanpassingen doen. Dit is de methode van Euler en is een numerieke methode om dit probleem op te lossen.
- Per klein tijdsinterval $dt$ kunnen we de aangepaste snelheid berekenen.
Vermits $F=m.a$ $F=m.a$ wil dit zeggen dat $a={\frac {F}{m}}$ $a={\frac {F}{m}}$
- Dus voor $F_{d}$ $F_{d}$ kunnen we dus stellen dat de (negatieve) versnelling door de luchtweerstand gelijk is aan:
  - $a_{d}={\frac {F_{d}}{m}}={\frac {1}{2}}{\frac {\rho v^{2}C_{d}A}{m}}$
- Deze versnelling (=vertraging want werkt in tegengestelde richting aan de snelheid van het voorwerp) kunnen we dan gebruiken om de snelheid
  - voor de x-component van de snelheid
    - $\Delta vx=-a_{d}dt$
    - $\Leftrightarrow v_{2}-v_{1}=-a_{d}dt$
    - $\Leftrightarrow v_{2}=v_{1}-a_{d}dt$
  - voor de y-component van de snelheid
    - hier werkt ook de valversnelling mee
    - $\Delta vy=-(g+a_{d})dt$
    - $\Leftrightarrow v_{2}-v_{1}=-(g+a_{d})dt$
    - $\Leftrightarrow v_{2}=v_{1}-(g+a_{d})dt$
  - Dus de nieuwe snelheid op $dt$ verder in de tijd wordt dus berekend op basis van de voorgaande snelheid + de kleine aanpassing. Door dit te doen vanaf de beginsnelheid en dit te herhalen over het gehele traject bekomen we dus de baan van de pijl met luchtweerstand.
- Een voorwerp dat naar beneden valt zal versnellen totdat het aan zijn eindsnelheid (terminal velocity) komt.. vanaf dat moment is de snelheid van het vallend voorwerp constant en versnelt het niet meer.
- De Eindsnelheid/Terminal velocity wordt weergegeven door de formule: $v_{term}={\sqrt {\frac {2m.g}{\rho AC_{d}}}}$
- In het computer programma dat we gebruiken om de baan van de pijl met luchtweerstand te berekenen, moeten we ook rekening houden dat indien de snelheid bij het terug naar beneden vallen groter zou worden dat de Eindsnelheid, om deze dus te beperken tot maximaal de Eindsnelheid/terminal velocity.
Wanneer we dit toepassen voor hoeken van 89, 75, 45 en 30 graden resulteert dit in volgende grafiek:

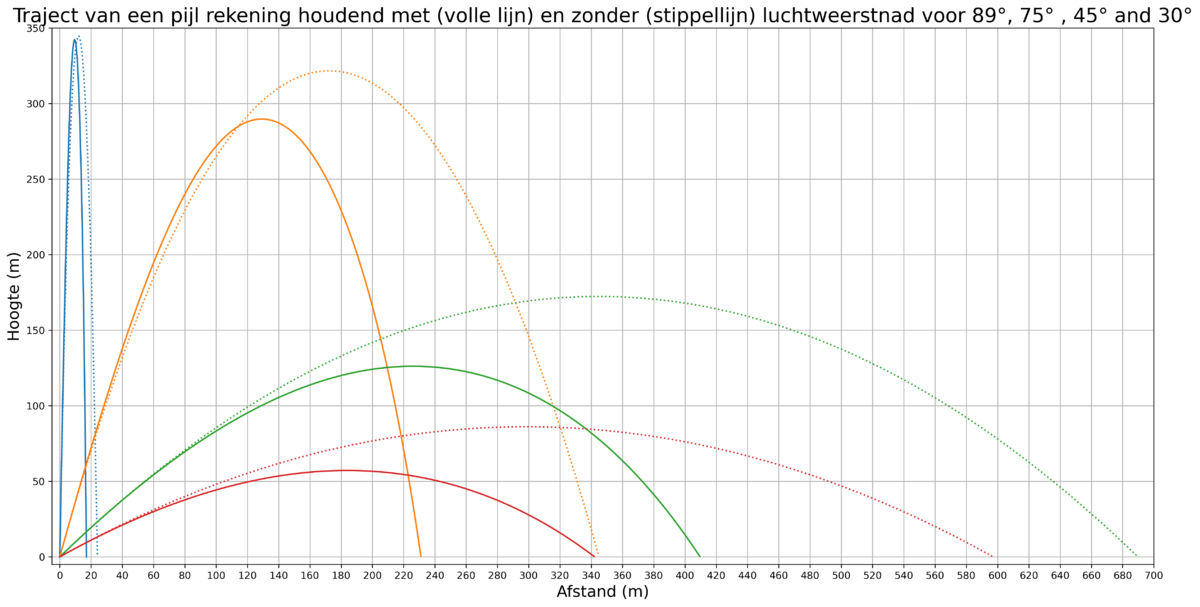
- Wat me nog niet helemaal duidelijk is, en dit kan een artefact zijn van de numerieke methode, is waarom het traject voor pijlen met hoeken groter dan 45° lager uitvallen in het begin dat de trajecten voor pijl met luchtweerstand. Misschien moet ik daar eens goed over slapen.

Python code

Syntaxhighlighting lijkt niet te werken, sorry.

<syntaxhighlight lang="python" line> def quick_sort(arr): less = [] pivot_list = [] more = [] if len(arr) <= 1: return arr else: pass ‎</syntaxhighlight>

imports

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt

helper functies

# Define helper functions
# KE
def kinetic_energy(m, v):
    return 0.5*(m*0.0647989/1000)*(v*0.3048)*(v*0.3048)
# momentum
def momentum(m, v):
    return (m*0.0647989/1000)*(v*0.3048)

def grain2gram(x):
    return x * 0.0647989

def grain2kg(x):
    return grain2gram(x)/1000

def gram2grain(x):
    return x / 0.0647989

def fps2ms(x):
    return x * 0.3048

def ms2fps(x):
    return x / 0.3048

def inch2meter(x):
    return(x*0.0254)
def meter2inch(x):
    return(x/0.0254)

def lbs2Newton(x):
    return(x*4.4482216)
def Newton2lbs(x):
    return(x/4.4482216)

Functies die het traject van de pijl met en zonder luchtweerstand berekenen

def simulate_trajectory(x0, y0, v0, theta, dt, num_timesteps, diameter, C_factor, air_density,  arrow_mass):
    """
    Simulates the trajectory of an arrow under the influence of air resistance.
    
    Parameters:
    x0 (float): initial x-coordinate of the arrow
    y0 (float): initial y-coordinate of the arrow
    v0 (float): initial velocity of the arrow
    theta (float): initial launch angle of the arrow (in radians)
    dt (float): time step size
    num_timesteps (int): number of timesteps to simulate
    
    Returns:
    xs (list of floats): x-coordinates of the arrow at each timestep
    ys (list of floats): y-coordinates of the arrow at each timestep
    """
    xs = [x0]
    ys = [y0]
    vs = [v0]
    vx = v0 * np.cos(theta)
    vy = v0 * np.sin(theta)
    vxs = [vx] # list of horizontal speeds
    vys = [vy] # List of vertical speeds
    
    A=np.pi*(diameter/2)**2
    g=9.81
    # include terminal velocity
    v_term=np.sqrt(2*arrow_mass*g/(air_density*A*C_factor))
#     print("The terminal velocity is: ",v_term)
    
    for i in range(num_timesteps):
        # Compute air resistance
        air_resistance_decelleration=0.5*air_density*A*C_factor*np.sqrt(vx**2 + vy**2) * vx / arrow_mass
        # F=m.a Dus a = F/m.. dus delen door arrow_mass om versnelling (negatief gebruiken) te krijgen
        # v² wordt berekend door sqrt van kwadraten van vx en vy, vermenigvuldig met vx omdat vx altijd positief is (of toch zou moeten zijn ;-)
        # print(air_resistance)
        # Update velocity
        vx = vx - (air_resistance_decelleration) * dt
        vy = vy - (g + air_resistance_decelleration ) * dt

#         print(vx, vy)
#         print(v0, vx,vy)
        # if the downward vertical speeds gets lower than the terminal velocity, make it the terminal velocity
        if vy < -1*v_term:
            vy= -1*v_term
#             print("terminal velocity reached ",v_term)
            print('y', end='') # add the end='' option in order not to go to a new line.
#         if ( (vx < v_term) and vy<=0 ):
#             vx= v_term
#             print('x', end='')
        # Update position
        xs.append(xs[-1] + vx * dt)
        ys.append(ys[-1] + vy * dt)
        # append also the speeds to the lists.. for debugging reasons...
        vs.append(np.sqrt(vx**2+vy**2))
        vxs.append(vx)
        vys.append(vy)
# We negeren Stokes nog even.. enkel bij trage snelheden...misschien later toevoegen
#         if (np.sqrt(vx**2+vy**2)*diameter)<0.015:
#             print("Stokes drag should be used!")
        if (ys[-1] + vy*dt) <= 0:  # stop simulation when vy becomes smaller than or equal to zero.. let arrow stop at ground
            break
#     return xs, ys, vs, vxs, vys
    return xs, ys

def simulate_trajectory_zonder(x0, y0, v0, theta, dt, num_timesteps, diameter, C_factor, air_density,  arrow_mass):
    """
    Simulates the trajectory of an arrow under the influence of air resistance.
    
    Parameters:
    x0 (float): initial x-coordinate of the arrow
    y0 (float): initial y-coordinate of the arrow
    v0 (float): initial velocity of the arrow
    theta (float): initial launch angle of the arrow (in radians)
    dt (float): time step size
    num_timesteps (int): number of timesteps to simulate
    
    Returns:
    xs (list of floats): x-coordinates of the arrow at each timestep
    ys (list of floats): y-coordinates of the arrow at each timestep
    """
    xs = [x0]
    ys = [y0]
    vs = [v0]
    vx = v0 * np.cos(theta)
    vy = v0 * np.sin(theta)
    vxs = [vx] # list of horizontal speeds
    vys = [vy] # List of vertical speeds
    
#     A=np.pi*(diameter/2)**2
    g=9.81
    # include terminal velocity
#     v_term=np.sqrt(2*arrow_mass*g/(air_density*A*C_factor))
#     print("The terminal velocity is: ",v_term)
    
    for i in range(num_timesteps):
        # Compute air resistance
#         air_resistance_decelleration=0.5*air_density*A*C_factor*np.sqrt(vx**2 + vy**2) * vx / arrow_mass
        # F=m.a Dus a = F/m.. dus delen door arrow_mass om versnelling (negatief gebruiken) te krijgen
        # v² wordt berekend door sqrt van kwadraten van vx en vy, vermenigvuldig met vx omdat vx altijd positief is (of toch zou moeten zijn ;-)
        # print(air_resistance)
        # Update velocity
#         vx = vx - (air_resistance_decelleration) * dt
#         vy = vy - (g + air_resistance_decelleration ) * dt
        vx = vx 
        vy = vy - (g ) * dt


#         print(vx, vy)
#         print(v0, vx,vy)
        # if the downward vertical speeds gets lower than the terminal velocity, make it the terminal velocity
#         if vy < -1*v_term:
#             vy= -1*v_term
#             print("terminal velocity reached ",v_term)
#             print('y', end='') # add the end='' option in order not to go to a new line.
#         if ( (vx < v_term) and vy<=0 ):
#             vx= v_term
#             print('x', end='')
        # Update position
        xs.append(xs[-1] + vx * dt)
        ys.append(ys[-1] + vy * dt)
        # append also the speeds to the lists.. for debugging reasons...
        vs.append(np.sqrt(vx**2+vy**2))
        vxs.append(vx)
        vys.append(vy)
# We negeren Stokes nog even.. enkel bij trage snelheden...misschien later toevoegen
#         if (np.sqrt(vx**2+vy**2)*diameter)<0.015:
#             print("Stokes drag should be used!")
        if (ys[-1] + vy*dt) <= 0:  # stop simulation when vy becomes smaller than or equal to zero.. let arrow stop at ground
            break
#     return xs, ys, vs, vxs, vys
    return xs, ys

#######################################################

== Eigenlijk programma om de plot aan te maken.

# Door deze parameters in een lijst te zetten kunnen we gemakkelijk verschillende grafieken maken door deze parameters aan te passen.
# hh=[89,75,45,30] # graden
hh=[89*np.pi/180,75*np.pi/180,45*np.pi/180,30*np.pi/180] # radials
mm=[grain2kg(550)]*4 # grains
CC=[1.42]*4 # drag coefficiënt
dd=[inch2meter(0.280)]*4 # diameter
rr=[1.3]*4 #kg/m^3 Air density
ss=[fps2ms(270)]*4

# Different values for Cd tested (drag coefficient)
# C=0.295 # Bullet https://en.wikipedia.org/wiki/Drag_coefficient
# C=1.65 # https://www.sciencedirect.com/science/article/pii/S1877705813010680#:~:text=The%20arrow%20launched%20by%20the,induces%20the%20boundary%20layer%20transition.
# C=0.9 # based on video, no fletching, https://www.youtube.com/watch?v=1L8r4hAgVsw
# C=1.42 # experimental by someone in a field
# The shape of the projectile influences its coefficient of drag, which determines how strongly air resistance affects an object's flight path. The higher the coefficient, the larger the effect. 
# For shapes, you can choose "none," which has zero drag; "wing shape," such as the wing of an airplane with a very low coefficient of 0.2; a "sphere," which has a coefficient of 0.5; 
# and a "flat plate," which is anything with a face of a large, flat surface area, with a coefficient of 1.28.
#

# Set initial conditions
g=9.81 #N/kg


# rho=1.3 #kg/m^3 Air density
launch_x = 0
launch_y = 0
stop_y=0

dt = 0.01  # time step size of 0.1 s
num_timesteps = 10000  # simulate for 1000 timesteps

# print("Check for Newtonian vs Strokes drag (must be more than about 0.015): ",v0*dd[0])

# volgorde parameters: (x0, y0, v0, theta, dt, num_timesteps, diameter, C_factor, air_density,  arrow_mass)

# labels
LANG='NL'

if LANG=='EN':
    my_x_axis_label='Distance (m)'
    my_y_axis_label='Height (m)'
    my_title='Trajectory of an arrow with (solid line) and without (dotted line) air resistance for 89°, 75° , 45° and 30° angles'
if LANG=='NL':
    my_x_axis_label='Afstand (m)'
    my_y_axis_label='Hoogte (m)'
    my_title='Traject van een pijl rekening houdend met (volle lijn) en zonder (stippellijn) luchtweerstnad voor 89°, 75° , 45° and 30°'
else:
    my_x_axis_label='X'
    my_y_axis_label='Y'
    my_title='Title'

    
fig, ax = plt.subplots(figsize=(20, 10))
ax.set_title(my_title,fontsize=20)
ax.set_xlabel(my_x_axis_label,fontsize=16)
ax.set_ylabel(my_y_axis_label,fontsize=16)

plt.xticks(np.arange(0, 860, 20) )

ymin=-5
ymax=350
ax.set_ylim(ymin, ymax)
ax.set_xlim(-5, 700)
# ax.axis('equal')
# default colors print(plt.rcParams['axes.prop_cycle'].by_key()['color'])
my_colors=[u'#1f77b4', u'#ff7f0e', u'#2ca02c', u'#d62728', u'#9467bd', u'#8c564b', u'#e377c2', u'#7f7f7f', u'#bcbd22', u'#17becf']


# Simulate trajectory
for index,hoek in enumerate(hh):
    my_x, my_y= simulate_trajectory(launch_x, launch_y, ss[index], hoek, dt, num_timesteps, dd[index] , CC[index], rr[index], mm[index])
#     steps=1000
#     how_far=max_distance(hoek*180/np.pi,ss[index],launch_y,stop_y)
#     my_range=np.arange(launch_x, how_far, (how_far-launch_x)/steps)
    # Plot trajectory
    plt.plot(my_x, my_y,color=my_colors[index])
    my_x, my_y= simulate_trajectory_zonder(launch_x, launch_y, ss[index], hoek, dt, num_timesteps, dd[index] , CC[index], rr[index], mm[index])
#     plt.plot(my_range,y_positie(hoek*180/np.pi, ss[index], launch_y, stop_y, launch_x, my_range),color=my_colors[index],linestyle='dotted' )
    plt.plot(my_x, my_y,color=my_colors[index],linestyle='dotted' )
    
plt.grid(True)
dpi=300
myfilename='Arrow_flight_with_Air_resistance_transparent_'+LANG+'_'+str(dpi)+'dpi.png'
plt.savefig(myfilename,dpi=300, bbox_inches='tight',transparent=True) 
plt.show()

De vlucht van een pijl zonder en met luchtweerstand: Difference between revisions

Revision as of 09:54, 6 January 2023

Contents

De vlucht van een pijl zonder luchtweerstand

Vlucht van de pijl rekening houdend met de luchtweerstand.

Python code

imports

helper functies

Functies die het traject van de pijl met en zonder luchtweerstand berekenen

Navigation menu

Page actions

Page actions

Personal tools

Navigation

Search

Tools

@@ Line 161: / Line 161: @@
 </pre>
-== main code ==
+== Functies die het traject van de pijl met en zonder luchtweerstand berekenen ==
 <pre>
 def simulate_trajectory(x0, y0, v0, theta, dt, num_timesteps, diameter, C_factor, air_density,  arrow_mass):
@@ Line 297: / Line 297: @@
 #######################################################
+</pre>
+== Eigenlijk programma om de plot aan te maken.
+<pre>
 # Door deze parameters in een lijst te zetten kunnen we gemakkelijk verschillende grafieken maken door deze parameters aan te passen.
 # hh=[89,75,45,30] # graden